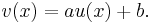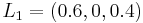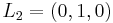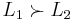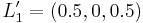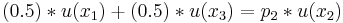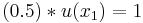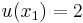Cardinal utility
In economics, cardinal utility refers to a property of mathematical indices that preserve preference orderings uniquely up to positive linear transformations.[1][2] Two utility indices are related by a linear transformation if for every value 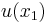 of one index u, occurring at quantity
of one index u, occurring at quantity 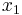 of the goods bundle being evaluated, the corresponding value
of the goods bundle being evaluated, the corresponding value 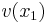 of the other index v satisfies a relationship of the form
of the other index v satisfies a relationship of the form
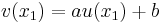 ,
,
for fixed constants a and b. Thus the utility functions themselves are related by
The two indices differ only with respect to scale and origin.[1]
Cardinal utility is mostly considered to be an outdated idea. Only within specific contexts such as decision making under risk, utilitarian welfare evaluations, and discounted utilities for intertemporal evaluations, cardinal utility is usually accepted.[3] Elsewhere, such as in general consumer theory, ordinal utility is preferred.
History
Modern work in cardinal utility theory began in the 18th century, when Daniel Bernoulli proposed a logarithmic utility function as a solution to the St. Petersburg paradox. Logarithmic utility accounts for the diminishing marginal utility of wealth since people consider money gains to be less and less satisfying the more they possess. Attaching an act of human beings (consuming monetary units) to a functional form (the logarithm) was a useful analogy, but it was yet to be linked to the theory of demand.
Jeremy Bentham believed that some complex introspective examination could somehow measure satisfaction or utility. Driven by a desire to establish "the principle of utility" as the basis of all legislation and social policy, Bentham wrote a manuscript circa 1782 where he defines the unit of intensity as "the degree of intensity possessed by that pleasure which is the faintest of any that can be distinguished to be pleasure"; he also stated that, as these pleasures are perceived to be more and more intense, they may be represented by higher and higher numbers.[4] In the 18th and 19th centuries the issue of the measurability of "utility" received plenty of attention from European schools of political economy, most notably through the work of William Stanley Jevons, Leon Walras and Alfred Marshall. Jevons defined utility as a useful object, or something which could increase pleasurable feeling or remove pain.[5] Nonetheless, he was characteristically frank and confused when referring to the measurability of utility, since he argued -in later editions of his works- that it was difficult to imagine how estimations of utility and summations can be made with any approach to accuracy.[4] Overall, there was an enthusiasm for measurement in the Victorian era, and there were many aspects of life succumbing to quantification.[6]
Supporters of cardinal utility theory in the 19th century suggested that the amount of utility obtained had to have a repercussion on the market price, although they did not say much about the problem of dealing with the subjectivity behind this alleged effect. Accurately measuring subjective pleasure (or pain) seemed awkward, and the thinkers of the time were aware of it; otherwise, they would not had renamed utility in imaginative ways such as subjective wealth, overall happiness, moral worth, psychic satisfaction, or ophélimité. During the second half of the 19th century, many studies related to this fictional magnitude -utility- were conducted, but the conclusion was always the same: unlike with distance or time, one cannot simply use a ruler or stopwatch to observe the number of "utils" obtained (that was the name actually given to the units in a utility scale). Not only it proved impossible to definitively say whether a good is worth 50, 75, or 125 utils to a person, or to two different people, but the mere dependence of utility on notions of hedonism, led academic circles to be skeptical of this theory.[7]
Francis Edgeworth felt necessary to ground the theory of utility into the real world. He discussed the quantitative estimates that a person can make of his own pleasure or the pleasure of others, borrowing methods developed in psychology to study hedonic measurement: psychophysics. This field of psychology was built on work by Ernst H. Weber, but its ideas were abandoned as the Stanley Steven's Power Law became more accepted.[8]
In the late 19th century, Carl Menger and his followers from the Austrian school of economics undertook the first successful departure from measurable utility, in the clever form of a theory of ranked uses. Despite abandoning the thought of quantifiable utility (i.e. psychological satisfaction mapped into the set of real numbers) Menger managed to establish a body of hypothesis about decision-making, resting solely on a few axioms of ranked preferences over the possible uses of goods and services.
Around the turn of the 19th century, a fraction of the marginalists known as the neoclassicals, started to embrace alternative ways to deal with the measurability issue. By 1900, Pareto was hesitant about accurately measuring pleasure or pain because he thought that such a self-reported subjective magnitude lacked scientific validity. He wanted to find an alternative way to treat utility that did not rely on erratic perceptions of the senses.[9]
The works and manuals of Vilfredo Pareto, Francis Edgeworth, Irving Fischer, and Eugene Slutsky, were pivotal to the development of utility theory. According to Viner,[10] these economic thinkers were striving to come up with a theory that would explain the negative slopes of demand curves. Their method consisted of rejecting the measurability of utility by pursuing the construction of some abstract indifference curve map.
The new theory of an ordinal utility was put together by John Hicks and Roy Allen in 1934,[11] in a seminal paper for the theory of consumer behaviour under perfect competition and certainty.
Measurability of utility and "cardinality"
A utility function is considered to be measurable, if the strength of preference or intensity of liking of a good or service is determined with precision by the use of some objective criteria. For example, suppose that the act of eating an apple gives to a person exactly half the pleasure of that of eating an orange. This would be a measurable utility if and only if the test employed for its direct measurement is based on an objective criterion that could let any external observer repeat the results accurately.[12] One hypothetical way to achieve this would be by the use of an hedonometer, which was the instrument suggested by Edgeworth to be capable of registering the height of pleasure experienced by people, diverging according to a law of errors.[8]
Before the 1930s, the measurability of utility functions was erroneously labeled as cardinality by economists. A different meaning of cardinality was used by economists who followed the formulation of Hicks-Allen. Under this usage, the cardinality of a utility function is simply the mathematical property of uniqueness up to a linear transformation. Around the end of the 1940s, some economists even rushed to argue that von Neumann-Morgenstern axiomatization of expected utility had resurrected measurability.[13]
The confusion between cardinality and measurability was not to be fully solved until the works of Armen Alchian,[14] William Baumol,[15] and John Chipman.[16] The title of Baumol's paper, "The cardinal utility which is ordinal", expressed well the semantic mess of the literature at the time. It is helpful to consider the same problem as it appears in the construction of scales of measurement in the natural sciences.[17] In the case of temperature there are two degrees of freedom for its measurement - the choice of unit and the zero. Different temperature scales map its intensity in different ways. In the celsius scale the zero is chosen to be the point where water freezes, and likewise, in cardinal utility theory one would be tempted to think that the choice of zero would correspond to a good or service that brings exactly 0 utils. However this is not necessarily true. The mathematical index remains cardinal, even if the zero gets moved arbitrarily to another point, or if the choice of scale is changed, or if both the scale and the zero are changed. Every measurable entity maps into a cardinal function but not every cardinal function is the result of the mapping of a measurable entity. The point of this example was used to prove that (as with temperature) it is still possible to predict something about the combination of two values of some utility function, even if the utils get transformed into entirely different numbers, as long as it remains a linear transformation.
The following quote from Alchian served to clarify once and for all the real nature of utility functions, emphasizing that they no longer need to be measurable:
Can we assign a set of numbers (measures) to the various entities and predict that the entity with the largest assigned number (measure) will be chosen? If so, we could christen this measure "utility" and then assert that choices are made so as to maximize utility. It is an easy step to the statement that "you are maximizing your utility", which says no more than that your choice is predictable according to the size of some assigned numbers. For analytical convenience it is customary to postulate that an individual seeks to maximize something subject to some constraints. The thing -or numerical measure of the "thing"- which he seeks to maximize is called "utility". Whether or not utility is of some kind glow or warmth, or happiness, is here irrelevant; all that counts is that we can assign numbers to entities or conditions which a person can strive to realize. Then we say the individual seeks to maximize some function of those numbers. Unfortunately, the term "utility" has by now acquired so many connotations, that it is difficult to realize that for present purposes utility has no more meaning than this.
—Armen Alchian, The meaning of utility measurement[14]
During the past decade, economists are having a renewed interest in the measurement issues of happiness.[18][19]
Preferences in cardinal utility theory
In 1955, Patrick Suppes and Muriel Winet solved the issue of the representability of preferences by a cardinal utility function, and derived the set of axioms and primitive characteristics required for this utility index to work.[20]
Suppose you are asked to rank your preferences of 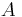 to
to 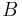 and your preferences of
and your preferences of 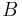 to
to 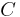 . If you find that you can state, for example, that your preference of
. If you find that you can state, for example, that your preference of 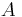 to
to 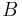 exceeds your preference of
exceeds your preference of 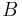 to
to 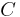 , we could summarize this information by any triplet of numbers satisfying the two inequalities: (a)
, we could summarize this information by any triplet of numbers satisfying the two inequalities: (a) 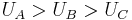 , and (b)
, and (b) 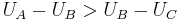 .
.
If 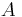 and
and 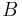 were sums of money, you could vary the sum of money represented by
were sums of money, you could vary the sum of money represented by 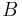 until you could tell us that you found your preference of
until you could tell us that you found your preference of 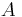 to
to 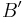 equal to your preference of
equal to your preference of 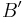 to
to 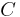 . If you find such a
. If you find such a 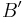 , then the results of this last operation would be expressed by any triplet of numbers satisfying the relationships: (a)
, then the results of this last operation would be expressed by any triplet of numbers satisfying the relationships: (a) 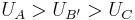 , and (b)
, and (b) 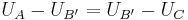 . Any two triplets obeying these relationships must be related by a linear transformation; they represent utility indices differing only by scale and origin. In this case, "cardinality" means nothing more being able to give consistent answers to these particular questions. Note that this experiment does not require measurability of utility. Itzhak Gilboa gives a sound explanation of why measurability can never be attained solely by introspection:
. Any two triplets obeying these relationships must be related by a linear transformation; they represent utility indices differing only by scale and origin. In this case, "cardinality" means nothing more being able to give consistent answers to these particular questions. Note that this experiment does not require measurability of utility. Itzhak Gilboa gives a sound explanation of why measurability can never be attained solely by introspection:
It might have happened to you that you were carrying a pile of papers, or clothes, and didn't notice that you dropped a few. The decrease in the total weight you were carrying was probably not large enough for you to notice. Two objects may be too close in terms of weight for us to notice the difference between them. This problem is common to perception in all our senses. If I ask whether two rods are of the same length or not, there are differences that will be too small for you to notice. The same would apply to your perception of sound (volume, pitch), light, temperature, and so forth...
—Itzhak Gilboa, Theory of decision under uncertainty[21]
According to this view, those situations where a person just can't tell the difference between 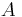 and
and 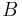 , will lead to indifference not because of a consistency of preferences, but because of a misperception of the senses. Moreover, human senses adapt to a given level of stimulation and then register changes from that baseline.[22]
, will lead to indifference not because of a consistency of preferences, but because of a misperception of the senses. Moreover, human senses adapt to a given level of stimulation and then register changes from that baseline.[22]
Applications to welfare economics
Among welfare economists of the utilitarist school it has been the general tendency to take satisfaction (in some cases, pleasure) as the unit of welfare. If the function of welfare economics is to contribute data which will serve the social philosopher or the statesman in the making of welfare judgements, this tendency leads perhaps, to a hedonistic ethics.[23]
Under this framework, actions (including production of goods and provision of services) are judged by their contributions to the subjective wealth of people. In other words, it provides a way of judging the "greatest good to the greatest number of persons". An act that reduces one person's utility by 75 utils while increasing two others' by 50 utils each has increased overall utility by 25 utils and is thus a positive contribution; one that costs the first person 125 utils while giving the same 50 each to two other people has resulted in a net loss of 25 utils. Some utilitarians thought that wealth could actually be redistributed to those with lower levels of utility. They also believed that, since utility has diminishing marginal returns, it could be transferred between people; for instance, if John is enjoying certain amount of utility, some of it can be shaven off the top of him and given to Joseph, who would find it more useful.
If a class of utility functions is cardinal, intrapersonal comparisons of utility differences are allowed. If, in addition, some comparisons of utility are meaningful interpersonally, the linear transformations used to produce the class of utility functions must be restricted across people. An example is cardinal unit comparability. In that information environment, admissible transformations are increasing affine functions and, in addition, the scaling factor must be the same for everyone. This information assumption allows for interpersonal comparisons of utility differences, but utility levels cannot be compared interpersonally because the intercept of the affine transformations may differ across people.[24]
Applications to marginal utility
- Under cardinal utility theory, the sign of the marginal utility of a good is the same for all the numerical representations of a particular preference structure.
- The magnitude of the marginal utility is not the same for all cardinal utility indices representing the same specific preference structure.
- The sign of the second derivative of a differentiable utility function that is cardinal, is the same for all the numerical representations of a particular preference structure. Given that this is usually a negative sign, there is room for a law of diminishing marginal utility in cardinal utility theory.
- The magnitude of the second derivative of a differentiable utility function is not the same for all cardinal utility indices representing the same specific preference structure.
Applications to expected utility theory
This type of indices involves choices under risk. In this case, 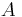 ,
, 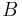 , and
, and 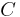 , are lotteries associated with outcomes. Unlike Cardinal utility theory under certainty, where the possibility of moving from preferences to quantified utility was almost trivial, here it is paramount to be able to map preferences into the set of real numbers, so that the operation of mathematical expectation can be executed. Once the mapping is done, the introduction of additional assumptions would result in a consistent behaviour of people regarding fair bets. But fair bets are, by definition, the result of comparing a gamble with an expected value of zero to some other gamble. Although it is impossible to model attitudes toward risk if one doesn't quantify utility, the theory should not be interpreted as measuring strength of preference under certainty.[25]
, are lotteries associated with outcomes. Unlike Cardinal utility theory under certainty, where the possibility of moving from preferences to quantified utility was almost trivial, here it is paramount to be able to map preferences into the set of real numbers, so that the operation of mathematical expectation can be executed. Once the mapping is done, the introduction of additional assumptions would result in a consistent behaviour of people regarding fair bets. But fair bets are, by definition, the result of comparing a gamble with an expected value of zero to some other gamble. Although it is impossible to model attitudes toward risk if one doesn't quantify utility, the theory should not be interpreted as measuring strength of preference under certainty.[25]
Suppose that certain outcomes are associated with three states of nature, so that 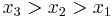 ; This set of outcomes,
; This set of outcomes, 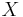 , can be assumed to be a calculable money-prize in a controlled game of chance, unique up to one positive proportionality factor depending on the currency unit.
, can be assumed to be a calculable money-prize in a controlled game of chance, unique up to one positive proportionality factor depending on the currency unit.
Let 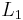 and
and 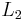 be two lotteries such that
be two lotteries such that
Assume that someone has the following preference structure under risk:
By modifiying the values of 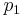 and
and 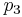 in
in 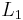 , eventually there will be some appropriate values (
, eventually there will be some appropriate values (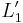 ) for which she is found to be indifferent between it and
) for which she is found to be indifferent between it and 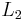 .
.
Expected utility theory tells us that:
Using the information of this example, Tapas Majumdar proved in a 1958 paper[26] that by fixing the arbitrary origin at 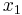 (the utility index being =0 at
(the utility index being =0 at 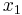 ), and by choosing the scale so that the utility index at
), and by choosing the scale so that the utility index at 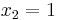 , then:
, then:
Thus the utility function is cardinal (it preserved the order of preference over 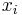 except for an arbitrary choice of origin and scale). This is the same as representing these preferences by a class of utility functions related only by linear transformations.
except for an arbitrary choice of origin and scale). This is the same as representing these preferences by a class of utility functions related only by linear transformations.
Applications to intertemporal utility
Models of utility with several periods, in which people discount future values of utility, need to employ cardinalism in order to have well-behaved utility functions.
Controversies
Some authors have commented on the ambiguity of the terms "cardinal utility" and "ordinal utility", as used in economic jargon:
These terms, which seem to have been introduced by Hicks and Allen (1934), bear scant if any relation to the mathematicians' concept of ordinal and cardinal numbers; rather they are euphemisms for the concepts of order-homomorphism to the real numbers and group-homomorphism to the real numbers
—John Chipman, The foundations of utility[16]
There remain economists who believe that utility can be measured. These measures are not perfect but can act as a proxy for the utility. Lancaster’s[27] characteristics approach to consumer demand illustrates this point.
See also
References
- ^ a b Ellsberg, Daniel. (1954). "Classic and current notions of 'Measurable utility'". Economic Journal 64(255): 528-556
- ^ Strotz, Robert. (1953). "Cardinal utility". American economic review Vol. 43, No. 2, pp. 384-397
- ^ Köbberling, Veronika. (2006). "Strength of preference and cardinal utility". Economic theory, No. 27, p. 375
- ^ a b Stigler, George. (1950). "The development of utility theory. I". Journal of political economy Vol. 58, No. 4, pp. 307-327
- ^ Jevons, William Stanley. (1866). "Brief account of a general mathematical theory of political economy".
- ^ Bernstein, Peter. (1996). Against the gods. The remarkable story of risk. New York: John Wiley and Sons, p. 191
- ^ Stigler, George. (1950). "The development of utility theory. II". Journal of political economy Vol. 58, No. 5, pp. 373-396
- ^ a b Colander, David. (2007). "Retrospectives: Edgeworth's hedonimeter and the quest to measure utility". Journal of economic perspectives, Vol. 21, No. 2, pp. 215-226.
- ^ Lewin, Shira. (1996). Economics and psychology: lessons for our own day from the early twentieth century". Journal of economic literature 34(3), 1293-1323.
- ^ Viner, Jacob. (1925a). "The utility concept in value theory and its critics". Journal of political economy Vol. 33, No. 4, pp. 369-387
- ^ Hicks, John and Roy Allen. (1934). "A reconsideration of the theory of value". Economica Vol. 1, No. 1, pp. 52-76
- ^ Bernadelli, H. (1938). "The end of the marginal utility theory". Economica, Vol. 5, No. 18, p. 196
- ^ Lewin, Shira. (1996). "Economics and psychology: lessons for our own day from the early twentieth century". Journal of economic literature 34 (3), 1293-1323.
- ^ a b Alchian, Armen. (1953). "The meaning of utility measurement". American economic review Vol. 43, No. 1, pp. 26-50.
- ^ Baumol, William. (1958). "The cardinal utility which is ordinal". Economic journal Vol. 68, No. 272, pp. 665-672
- ^ a b Chipman, John. (1960). "The foundations of utility". Econometrica Vol. 28, No. 2, pp. 215-216
- ^ Allen, Roy. (1935). "A note on the determinateness of the utility function". Review of economic studies, Vol. 2, No. 2, pp. 155-158
- ^ Kahneman, Daniel., Peter Wakker, and Rakesh Sarin. (1997). "Back to Bentham? Explorations of experienced utility?". Quarterly journal of economics Vol. 112, No. 2, pp. 375-405.
- ^ Kahneman, Daniel., Ed Diener and Norbert Schwarz. (1999). Well-being: the foundations of hedonic psychology. New York: Rusell Sage Foundation
- ^ Suppes, Patrick and Muriel Winet. (1955). "An axiomatization of utility based on the notion of utility differences". Management scienceNo. 1, pp. 259-270
- ^ Gilboa, Itzhak. (2008). Theory of Decision under uncertainty. Cambridge University Press.
- ^ Poundstone, William. (2010). Priceless. The myth of fair value (and how to take advantage of it). New York: Hill and Wang, p. 39
- ^ Viner, Jacob. (1925b). "The utility concept in value theory and its critics. II. The utility concept in welfare economics". Journal of political economy Vol. 33, No. 6, pp. 638-659.
- ^ Blackorby, Charles., Walter Bossert and David Donaldson. (2002). "Utilitarianism and the theory of justice", in: Kenneth Arrow, Amartya Sen and Kotaru Suzumura (eds.) Handbook of social choice and welfare. Vol. 1 p. 552
- ^ Shoemaker, Paul. (1982). "The expected utility model: its variants, purposes, evidence and limitations". Journal of economic literature, Vol. 20, No. 2, pp. 529-563
- ^ Majumdar, Tapas. (1958). "Behaviourist cardinalism in utility theory". Economica, Vol. 25, No. 97, pp. 26-33
- ^ Lancaster, Kelvin. (1966). "A new approach to consumer theory". Journal of political economy Vol. 74, No. 2, pp. 132-157
External links
- Ordinal utility vs. Cardinal utility